#PYTHON(DAY10)Methods unique to sets

 

#PYTHON(DAY10)

Methods unique to sets

The methods in sets are:

1. union()
2. Intersection
3. difference
4. symmetric_difference
5. intersection_update
6. difference_update
7. symmetric_difference_update
8. isdisjoint, issubset, issuperset

union()

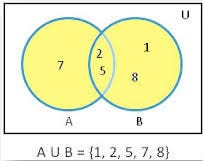
The union() method returns a set that contains all items from the original set, and all items from the specified set(s).

You can specify as many sets you want, separated by commas.

It does not have to be a set, it can be any iterable object.

If an item is present in more than one set, the result will contain only one appearance of this item.

union of sets

a = set({1,2,3,4,5})
b = set({4,5,6,7,8})
c = a.union(b)
d = b.union(a)
print(a,b,c,d, sep = '\n')

And the output is:

{1, 2, 3, 4, 5}
{4, 5, 6, 7, 8}
{1, 2, 3, 4, 5, 6, 7, 8}
{1, 2, 3, 4, 5, 6, 7, 8}

intersection()

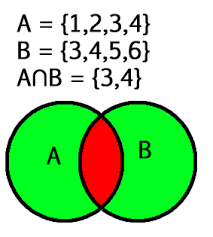
The intersection() method returns a set that contains the similarity between two or more sets.

Meaning: The returned set contains only items that exist in both sets, or in all sets if the comparison is done with more than two sets.

Intersection of sets

a = set({1,2,3,4,5})
b = set({4,5,6,7,8})
c = a.intersection(b)
d = b.intersection(a)
print(a,b,c,d, sep = '\n')

And the output is:

{1, 2, 3, 4, 5}
{4, 5, 6, 7, 8}
{4, 5}
{4, 5}

difference()

• it just removes the common elements in the set

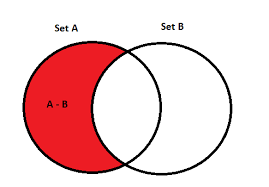
The difference() method returns a set that contains the difference between two sets.

Meaning: The returned set contains items that exist only in the first set, and not in both sets.

difference of sets

a = set({1,2,3,4,5})
b = set({4,5,6,7,8})
c = a.difference(b)
d = b.difference(a)
print(a,b,c,d, sep = '\n')

And the output is:

{1, 2, 3, 4, 5}
{4, 5, 6, 7, 8}
{1, 2, 3}
{8, 6, 7}

Symmetric_difference():

it removes the common elements from the set and gives the combination of remaining elements in the set

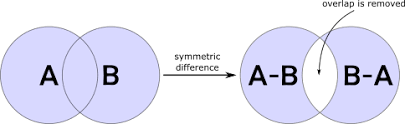
The symmetric_difference() method returns a set that contains all items from both set, but not the items that are present in both sets.

Meaning: The returned set contains a mix of items that are not present in both sets.

a = set({1,2,3,4,5})
b = set({4,5,6,7,8})
c = a.symmetric_difference(b)
d = b.symmetric_difference(a)
e = set()
print(a,b,c,d, sep = '\n')

And the output is:

{1, 2, 3, 4, 5}
{4, 5, 6, 7, 8}
{1, 2, 3, 6, 7, 8}
{1, 2, 3, 6, 7, 8}

intersection_update():

The intersection_update() method removes the items that is not present in both sets (or in all sets if the comparison is done between more than two sets).

The intersection_update() method is different from the intersection() method, because the intersection() method returns a new set, without the unwanted items, and the intersection_update() method removes the unwanted items from the original set.

a = set({1,2,3,4,5})
b = set({4,5,6,7,8})
print(a,b, sep = '\n')
a.intersection_update(b)
b.intersection_update(a)
print(a,b, sep = '\n')

And the output is:

{1, 2, 3, 4, 5}
{4, 5, 6, 7, 8}
{4, 5}
{4, 5}

difference_update():

It will calculate the difference of twosets and update the value of set, it is called upon

The difference_update() method removes the items that exist in both sets.

The difference_update() method is different from the difference() method, because the difference() method returns a new set, without the unwanted items, and the difference_update() method removes the unwanted items from the original set.

a = set({1,2,3,4,5})
b = set({4,5,6,7,8})
print(a,b, sep = '\n')
a.difference_update(b)
b.difference_update(a)
print(a,b, sep = '\n')

And the output is:

{1, 2, 3, 4, 5}
{4, 5, 6, 7, 8}
{1, 2, 3}
{4, 5, 6, 7, 8}

symmetric_difference_update():

It will calculate the symmetric_difference of twosets and update the value of set, it is called upon

The symmetric_difference_update() method updates the original set by removing items that are present in both sets, and inserting the other items.

a = set({1,2,3,4,5})
b = set({4,5,6,7,8})
print(a,b, sep = '\n')
a.symmetric_difference_update(b)
print(a,b, sep = '\n')

And the output is:

{1, 2, 3, 4, 5}
{4, 5, 6, 7, 8}
{1, 2, 3, 6, 7, 8}
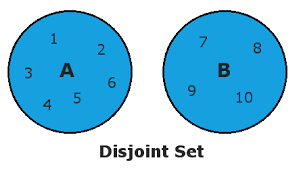
{4, 5, 6, 7, 8}

isdisjoint():

The isdisjoint() method returns True if none of the items are present in both sets, otherwise it returns False.

disjoint set

x = {"apple", "banana", "cherry"}
y = {"google", "microsoft", "apple"}

z = x.isdisjoint(y)

print(z)

And the output is:

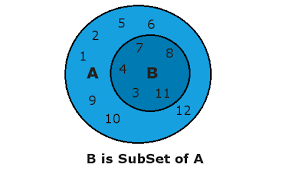
False

issubset():

The issubset() method returns True if all items in the set exists in the specified set, otherwise it returns False.

subset

x = {"a", "b", "c"}
y = {"f", "e", "d", "c", "b"}

z = x.issubset(y)

print(z)

And the output is:

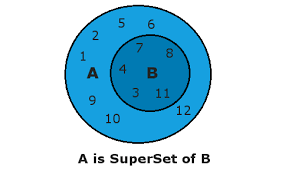
False

issuperset():

The issuperset() method returns True if all items in the specified set exists in the original set, otherwise it returns False.

superset

x = {"f", "e", "d", "c", "b"}
y = {"a", "b", "c"}

z = x.issuperset(y)

print(z)

And the output is:

False

#PYTHON(DAY9)Sets and it's methods

 

#PYTHON(DAY9)

Sets and it’s methods

sets

• sets are a cluster of data values, they are not ordered
• we declare sets by using ‘{ }’
• sets do not have duplicate values
• we can use set class to perform task
• sets have methods that are unique to sets, like union, intersection etc
• to create an empty set, use set(). using {} gives an empty dictionary

x = {1,2,3,4, print, 'three'}
print(x, len(x), type(x), sep ='\n')

And the expected output is:

{1, 2, 3, 4, <built-in function print>, 'three'}
6
<class 'set'>

creating set with one element:

x = {8}
print(x)

And the expected output is:

{8}

Note: As, in tuples there is no need to place “ , “, for creating set with one element

Sets can not have duplicate elements

a = 'malayalam'
x = set(a)
print(x, len(x), type(x), sep = '\n')

And the expetced output is:

{'l', 'm', 'a', 'y'}
4
<class 'set'>

sets have no order in python

x = set()
print(x)

And the expected output is:

set()

Methods in set

Python has a set of built-in methods that you can use on sets

print(dir(set))

And the list methods are:

['__and__', '__class__', '__class_getitem__', '__contains__', '__delattr__', '__dir__', '__doc__', '__eq__', '__format__', '__ge__', '__getattribute__', '__gt__', '__hash__', '__iand__', '__init__', '__init_subclass__', '__ior__', '__isub__', '__iter__', '__ixor__', '__le__', '__len__', '__lt__', '__ne__', '__new__', '__or__', '__rand__', '__reduce__', '__reduce_ex__', '__repr__', '__ror__', '__rsub__', '__rxor__', '__setattr__', '__sizeof__', '__str__', '__sub__', '__subclasshook__', '__xor__', 'add', 'clear', 'copy', 'difference', 'difference_update', 'discard', 'intersection', 'intersection_update', 'isdisjoint', 'issubset', 'issuperset', 'pop', 'remove', 'symmetric_difference', 'symmetric_difference_update', 'union', 'update']

Now, let’s talk about some of the important methods in set

add()

• it adds exactly one element to the set

x = {1,2,3,4}
x.add(6)
print(x)

output is:
{1, 2, 3, 4, 6}

x.add(5)
print(x)

output is:
{1, 2, 3, 4, 5, 6}

add() takes exactly one element only

pop()

• it is going to pop a random element, pop in sets takes no input/arg

print(x)
a = x.pop()
print(x,a, sep ='\n')

output is:
{1, 2, 3, 5}
{2, 3, 5}
1

copy()

a = set('hellow world!')
b = a
print(a,b, sep = '\n')
print()
a.update(['xx','yy'])
print(a,b, sep = '\n')
print()

output is:
{'!', 'h', 'o', 'w', ' ', 'd', 'l', 'e', 'r'}
{'!', 'h', 'o', 'w', ' ', 'd', 'l', 'e', 'r'}

{'!', 'h', 'yy', 'xx', 'o', 'w', ' ', 'd', 'l', 'e', 'r'}
{'!', 'h', 'yy', 'xx', 'o', 'w', ' ', 'd', 'l', 'e', 'r'}

a = set('hellow world!')
b = a.copy()
print(a,b, sep = '\n')
print()
a.update(['xx','yy'])
print(a,b, sep = '\n')
print()

output is:
{'!', 'h', 'o', 'w', ' ', 'd', 'l', 'e', 'r'}
{'!', 'h', 'o', 'w', ' ', 'd', 'l', 'e', 'r'}

{'!', 'h', 'yy', 'xx', 'o', 'w', ' ', 'd', 'l', 'e', 'r'}
{'!', 'h', 'o', 'w', ' ', 'd', 'l', 'e', 'r'}

clear()

• clear() is used to clear the set

print(b)
b.clear()
print(b)

output is:
set()
set()

#PYTHON(DAY8)tuple and it's methods

 

#PYTHON(DAY8)

Tuple and It’s methods

Tuple()

• Tuples are sequential, indexable, heterogeneous containers which are immutable in nature
• ‘( )’ are used to represent a tuple, tuple can never be empty, it takes atleast 2 values
• a tuple with one element can be created using ‘,’ and passing no second element
• there are two methods we can perform on tuple
• we can use tuple as unpack
• tuples are faster when compared to list

Example:

mytuple = ("apple", 1,2)
print(mytuple)

And the output is:

('apple',1,2)

So, to know the type of class we use type() function

x = (1,2,3,1,'sree',4)
print(x)
print(type(x))

And the expected output is:

(1,2,3,1,'sree',4)
<class 'tuple'>

Tuple Length

To determine how many items a tuple has, use the len() function

thistuple = ("apple", "banana", "cherry")
print(len(thistuple))

And the expected output is:

3

creating an empty tuple

x = ()
print(x, len(x), type(x), sep = '\n')

And the expected output is:

()
0
<class 'tuple'>

creating a tuple with 2 elements

x = (1,)
print(x, len(x), type(x), sep = '\n')

And the expected output is:

(1,)
1
<class 'tuple'>

NOTE: tuple does not contain a single element

x = (1)
print(x, len(x), type(x), sep = '\n')

we get an error for this as: object of type ‘int’ has no len()

type-casting

converting list to tuple

a = [1,2,3]
x = tuple(a)
print(x, len(x), type(x), sep = '\n')

And the expected output is:

(1, 2, 3)
3
<class 'tuple'>

converting string to tuple

a = 'generic string'
x = tuple(a)
print(x, len(x), type(x), sep = '\n')

And the expected output is:

('g', 'e', 'n', 'e', 'r', 'i', 'c', ' ', 's', 't', 'r', 'i', 'n', 'g')
14
<class 'tuple'>

Access Tuple Items

You can access tuple items by referring to the index number, inside square brackets:

thistuple = ("apple", "banana", "cherry")
print(thistuple[1])

And the expected output is:

banana

The first item has index as 0

Negative Indexing

Negative indexing means start from the end.

-1 refers to the last item, -2 refers to the second last item etc.

thistuple = ("apple", "banana", "cherry")
print(thistuple[-1])

And the output is:

cherry

Methods in tuple():

1. index()
2. count()

Range of Indexes

You can specify a range of indexes by specifying where to start and where to end the range.

When specifying a range, the return value will be a new tuple with the specified items.

x = ('apple','banana','grapes','mango','orange','kiwi')
print([2:5])

And the expected output is:

('grapes','mango','orange')

Note: The search will start at index 2 (included) and end at index 5 (not included).

By leaving out the start value, the range will start at the first item:

thistuple = ("apple", "banana", "cherry", "orange", "kiwi", "melon", "mango")
print(thistuple[:4])

And the expected output is:

('apple', 'banana', 'cherry', 'orange')

Range of Negative Indexes

Specify negative indexes if you want to start the search from the end of the tuple:

This example returns the items from index -4 (included) to index -1 (excluded)

thistuple = ("apple", "banana", "cherry", "orange", "kiwi", "melon", "mango")
print(thistuple[-4:-1])

And the expected output is:

('orange', 'kiwi', 'melon')

Check if Item Exists

To determine if a specified item is present in a tuple use the in keyword:

Check if “apple” is present in the tuple:

thistuple = ("apple", "banana", "cherry")
if "apple" in thistuple:
  print("Yes, 'apple' is in the fruits tuple")

And the expected output is:

Yes, 'apple' is in the fruits tuple

count()

Returns the number of times the value appears in the tuple

thistuple = (1, 3, 7, 8, 7, 5, 4, 6, 8, 5)

x = thistuple.count(5)

print(x)

And the expected output is:

2

Unpacking a tuple

we can also extract the values back into variables. This is called “unpacking”

fruits = ("apple", "banana", "cherry")

(green, yellow, red) = fruits

print(green)
print(yellow)
print(red)

And the expected output is:

apple
banana
cherry